Question

Show that each of the following values for the given variable is a solution to the

given equation. Show the calculations that lead to your answer.
(a) 3x + 4 = 7
for x = 1

Answer 1

Part a)

Answer:

As the L.H.S = R.H.S, so
`x = 1` is the solution to the equation
`3x + 4 = 7`

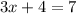
Explanation:

Given the equation

`3x + 4 = 7`

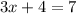
solving the equation for x = 1

substituting the value of x = 1 in the equation

`3\left(1\right)+\:4\:=\:7`

`7=7`

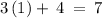
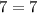
As the L.H.S = R.H.S, so
`x = 1` is the solution to the equation
`3x + 4 = 7`

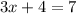
Part b)

Answer:

As the L.H.S = R.H.S, so
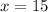`x = 15` is the solution to the equation
`(x-3)/(2)=6`

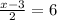
Explanation:

Given the equation

`(x-3)/(2)=6`

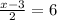
solving the equation for x = 15

substituting the value of x = 15 in the equation

`(15-3)/(2)=6`

`(12)/(2)=6`

`6=6`

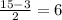
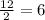
As the L.H.S = R.H.S, so
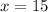`x = 15` is the solution to the equation
`(x-3)/(2)=6`

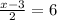
Part c)

Answer:

As the L.H.S = R.H.S, so x = -3 in the equation is the solution to the equation
`x^2=-2x+3`

Explanation:

Given the equation

`x^2=-2x+3`

solving the equation for x = -3

substituting the value of x = -3 in the equation

`x^2=-2x+3`

`\left(-3\right)^2=-2\left(-3\right)+3`

`9 = 6 + 3`

`9 = 9`

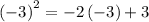
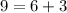
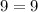
As the L.H.S = R.H.S, so x = -3 in the equation is the solution to the equation
`x^2=-2x+3`