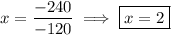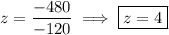Looks like the system is
x + 4y - z = -14
5x + 6y + 3z = 4
-2x + 7y + 2z = -17
or in matrix form,

Cramer's rule says that

where
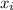 is the solution for i-th variable, and
is the solution for i-th variable, and
 is a modified version of
is a modified version of
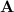 with its i-th column replaced by
with its i-th column replaced by
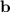 .
.
We have 4 determinants to compute. I'll show the work for det(A) using a cofactor expansion along the first row.
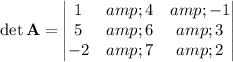
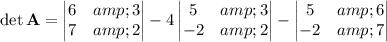
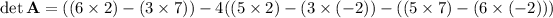
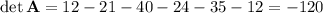
The modified matrices and their determinants are

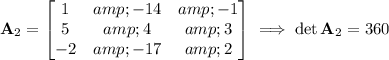
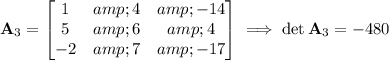
Then by Cramer's rule, the solution to the system is