Question

During a medieval siege of a castle, the attacking army uses a trebuchet to hurl heavy stones at the castle walls. If the trebuchet launches the stones with a velocity of +48.5" m"/s at an angle of 42.0°, how long does it take the stone to hit the ground? For those settings, what is the maximum range? How high will the stones go? Show all your work

Answer 1

a) t = 6.62 s

b) x = 238.6 m

c) H = 53.7 m

Step-by-step explanation:

a) We can find the time of flight as follows:

`y_(f) = y_(0) + v_{0_(y)}t - (1)/(2)gt^(2)`

Where:

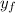`y_(f)` is the final height = 0

`y_(0)` is the initial height = 0

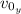`v_{0_(y)}` is the initial vertical velocity of the stone

t: is the time

g: is the gravity = 9.81 m/s²

`v_(0)sin(42)t - (1)/(2)gt^(2) = 0`

`48.5 m/s*sin(42)*t - (1)/(2)9.81 m/s^(2)*t^(2) = 0`

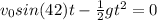
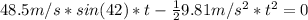
By solving the above quadratic equation we have:

t = 6.62 s

b) The maximum range is:

`x = v_{0_(x)}t = 48.5 m/s*cos(42)*6.62 s = 238.6 m`

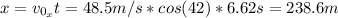
c) The maximum height (H) can be found knowing that at this height the final vertical velocity of the stone is zero:

`v_{f_(y)}^(2) = v_{0_(y)}^(2) - 2gH`

`H = \frac{v_{0_(y)}^(2) - v_{f_(y)}^(2)}{2g} = ((48.5 m/s*sin(42))^(2) - 0)/(2*9.81 m/s^(2)) = 53.7 m`

I hope it helps you!