Question

PROBLEM: (IF YOU TROLL I WILL REPORT) Riley has a rectangular shaped patio that is 13 feet long by 15 feet wide. He wants to DOUBLE THE AREA of the patio by increasing the length and width by the same amount. (200 POINTS)

1. Write an EQUATION that represents the total area of Riley's proposed patio.

2. To the NEAREST TENTH of a foot, what is the LENGTH and WIDTH of the new patio?

THANK YOU!!

Answer 1

Part A)

`390=(15+x)(13+x)`

Part B)

Approximately 18.77 feet long by 20.77 feet wide.

Explanation:

Currently, the patio is 13 feet long by 15 feet wide. Therefore, the area right now is:

`A=13(15)=195\text{ feet}^2`

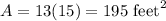
We will increase the length and width of the patio by the same amount such that the new area is double the previous amount.

Part 1)

The previous area is 195. Therefore, we would like to the new area to be twice of that. Hence, the new area is:

`A=2(195)=390`

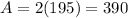
We will increase the length and the width by the same amount. Let’s call this amount x. Then by the area formula (A=bh), we can write:

`390=(15+x)(13+x)`

390 represents the doubled area. (15+x) is the width after the increase x, and (13+x) is the length after the same x increment.

Part 2)

So, we will solve for x. First, expand:

`390=195+15x+13x+x^2`

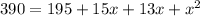
Simplify:

`x^2+28x+195=390`

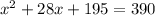
Subtract 390 from both sides:

`x^2+28x-195=0`

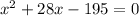
This is a quadratic. Hence, we can use the quadratic formula:

`x=(-b\pm√(b^2-4ac))/(2a)`

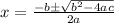
Our a=1, b=28, and c=-195. Hence:

`x=(-28\pm√((28)^2-4(1)(-195)))/(2(1))`

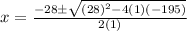
Evaluate:

`x=(-28\pm√(1564))/(2)`

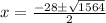
Simplify the square root:

`√(1564)=√(4)\cdot√(391)=2√(391)`

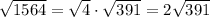
Hence:

`x=(-28\pm2√(391))/(2)\\`

Simplify:

`x=-14+√(391) \text{ or } -14-√(391)`

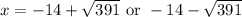
Approximate:

`x\approx5.77\text{ or } x\approx-33.77`

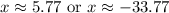
In this case, we can reject the negative solution.

Hence, the value of x is 5.77.

This means that we should increase the our length and width by 5.77.

Hence, the new length will be 13+5.77 or about 18.77.

And our new width will be 15+5.77 or about 20.77.

So, the new dimensions is approximately 18.77 by 20.77