Question

Determine what type of number the solutions are and how many exist for the equation 3x^2+7x+5=0

Answer 1

Two complex (imaginary) solutions.

Explanation:

To determine the number/type of solutions for a quadratic, we can evaluate its discriminant.

The discriminant formula for a quadratic in standard form is:

`\Delta=b^2-4ac`

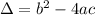
We have:

`3x^2+7x+5`

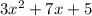
Hence, a=3; b=7; and c=5.

Substitute the values into our formula and evaluate. Therefore:

`\Delta=(7)^2-4(3)(5) \\ =49-60\\=-11`

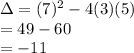
Hence, the result is a negative value.

If:

• The discriminant is negative, there are two, complex (imaginary) roots.
• The discriminant is 0, there is exactly one real root.
• The discriminant is positive, there are two, real roots.

Since our discriminant is negative, this means that for our equation, there exists two complex (imaginary) solutions.