Question

Choose the best answer:

the area of a right triangle is 12in^2. the ratio of the length of its legs is 2:3. Find the length of the hypotenuse.
a) square root is 13 in
b) 26 inches
c) 2 square root of 13
d) 52 inches
e) 4 square root of 13
​

Answer 1

The length of the hypotenuse is 2 square root of 13 ⇒ c

Explanation:

The rule of the area of the right triangle is A =
`(1)/(2)` × leg1 × leg2, where

leg1 and leg2 are the sides of the right angle

∵ The area of a right triangle is 12 in²

∵ The ratio of the length of its legs is 2: 3

→ Let leg1 = 2x and leg2 = 3x

∵ leg1 = 2x and leg2 = 3x

→ Substitute them in the rule of the area above

∴ 12 =
`(1)/(2)` × 2x × 3x

∵ 2x × 3x = 6x²

∴ 12 =
`(1)/(2)` × 6x²

∴ 12 = 3x²

→ Divide both sides by 3 to find x²

∴ 4 = x²

→ Take √ for both sides

∴ x = 2

→ Substitute x in the expressions of leg1 and leg2 to find them

∴ leg1 = 2(2) = 4 inches

∴ leg2 = 3(2) = 6 inches

∵ hypotenuse =
`\sqrt{(leg1)^(2)+(leg2)^(2)}`

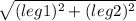
∴ hypotenuse =
`\sqrt{(4)^(2)+(6)^(2)}=√(16+36)=√(52)`

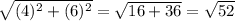
∵ The simplest form of
`√(52)` = 2
`√(13)`

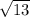
∴ The length of the hypotenuse = 2
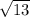`√(13)` inches