The question is incomplete.Here is the complete question.
The load that can be supported by a rectangular beam varies jointly as the width of the beam and the square of its length, and inversely as the length of the beam. A beam 13 feet long, with a width of 6 inches and a height of 4 inches can support a maximum load of 800 pounds. If a similar board has a width of 8 inches and a height of 7 inches, how long must it be to support 1300 pounds?
Answer: It must be 392 inches or approximately 33 feet.
Explanation: According to the question, the measures (width, length and height) of a beam and the weight it supports are in a relation of proportionality, i.e., if divided, the result is a constant.
For the first load:
width = 6in
height = 4in
length = 13ft or 156in
weight = 800lbs
Then, constant will be:
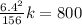

k = 1300
For the similar beam:
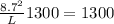
L = 49.8
L = 392in or 32.8ft
A similar board will support 1300lbs if it has 392 inches or 32.8 feet long.