Question

A tracking station lies at the origin of a coordinate system with the x-axis due east, the y-axis due north and the z-axis vertically upwards. Two aircraft have coordinates (20,25,11) and (26,31,12) relative to the tracking station.

a) find the distance between the two aircraft at the time.
b) the radar at the tracking station has a range of 40 km. Determine whether it will be able to detects both aircraft.

Answer 1

a) The distance between the two aircraft is approximately 8.544 km

b) The radar will not be able to detect the aircraft located at (26, 31, 12), which is approximately 42.20 km from the tracking station

Explanation:

The given parameters are;

The coordinates of the two aircraft are;

(20, 25, 11) and (26, 31, 12), which are the (x, y, z) coordinates

The distance between two points given the x, y, and z coordinates is given as follows;

`Distance \ between \ points = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2) +\left (z_(2)-z_(1) \right )^(2)}`

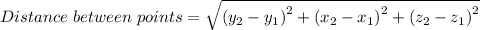
Therefore, we have;

`Distance \ between \ the \ two \ aircraft = \sqrt{\left (31-25 \right )^(2)+\left (26-20 \right )^(2) +\left (12-11 \right )^(2)}`

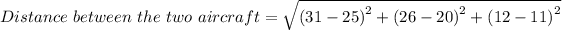
The distance between the two aircraft = √(6² + 6² + 1²) = √73 ≈ 8.544 km

b) The distance of both aircraft from the tracking station are given as follows;

For the first aircraft, we have;

`Distance \ between \ the \ first \ aircraft \ and \ station = \sqrt{\left (25-0 \right )^(2)+\left (20-0 \right )^(2) +\left (11-0 \right )^(2)}`

The distance between the first aircraft from the tracking station = √(25² + 20² + 11²) ≈ 33.853 km

Similarly, the distance between the second aircraft from the tracking station = √(26² + 31² + 12²) ≈ 42.20 km

Therefore, the second aircraft location is beyond the radar and the tracking station will not be able to detect the second aircraft