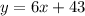Question

Write the equation of a line that is parallel to y = 6x +1 and that passes through the point (-7,1).

Answer 1

`y=6x+43`

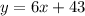
Explanation:

We want the equation of a line that is parallel to
`y=6x+1` which also passes through (-7, 1).

Since the new line is parallel, it must have the same slope as the original line.

The slope of the original line is 6.

Hence, the slope of our new line must also be 6.

We know that the slope is 6.

And it passes through the point (-7, 1).

So, we can use the point-slope form:

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point.

Substitute:

`y-1=6(x-(-7))`

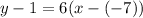
Simplify:

`y-1=6(x+7)`

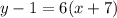
Distribute:

`y-1=6x+42`

Add 1 to both sides. Hence, our equation is:

`y=6x+43`