Question

Please help it’s attached please

Answer 1

The 17th term number of the arithmetic sequence will be: -97

i.e.

• 
  `a_(17)=-97`

Explanation:

Given the arithmetic sequence

`a_n=-6n+5`

Put
`n=17` in the arithemetic sequence to get the 17th term number

`a_(17)=-6\left(17\right)+5`

`a_(17)=-6\cdot \:17+5`

`a_(17)=-102+5`

`a_(17)=-97`

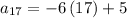
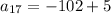
Therefore, the 17th term number of the arithmetic sequence will be: -97

i.e.

`a_(17)=-97`