Question

Find the distance from point A(−14, 5) to the line −x+2y = 14.

Answer 1

The distance from point A to given line is: 2√5 or 4.472 units

Explanation:

Given equation of line is:

`-x+2y= 14`

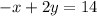
And the point is:

`A = (x_1,y_1) = (-14,5)`

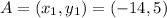
The standard form of equation of line is:

`Ax+By+C = 0`

Converting the given equation into standard form

`-x+2y-14=0`

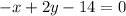
The distance of a point (x1,y1) from a line is given by the formula:

`d = (|Ax_1+By_1+C)/(√(A^2+B^2))`

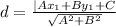
In the given details,

A = -1, B = 2, C = -14

x1 = -14, y1 = 5

Putting the values in the formula

`d = (|(-1)(-14)+(2)(5)-14|)/(√((-1)^2+(2)^2))\\d = (14+10-14)/(√(1+4))\\d = (10)/(√(5))\\d = (5*2)/(√(5))\\d = (√(5)*√(5)*2)/(√(5))\\d = 2√(5)\\d = 4.472\ units`

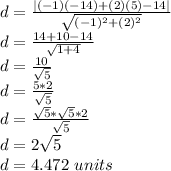
Hence,

The distance from point A to given line is: 2√5 or 4.472 units