Given:
The volume of the rectangular prism is
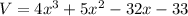
Two dimensions are (x+1) and (x+3).
To find:
The missing dimension.
Solution:
We know that, volume of a rectangular prism is
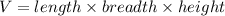
It means, volume of a rectangular prism is the product of all dimensions.
We have,
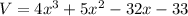
Splitting the middle terms, we get
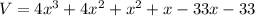
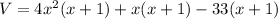
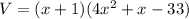
Splitting the middle term, we get
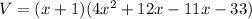
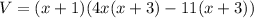
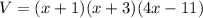
So, the three dimensions of the rectangular prism are (x+1), (x+3) and (4x-11).
Therefore, the missing dimension is (4x-11).