Question

A) write an explicit formula for the sequence 12, 16, 20, 24 B) Find the 11th term of the sequence *

Answer 1

A) The explicit formula for the sequence is
`f(n) = 12+4\cdot n`,
`n \in \mathbb{N}_(O)`.

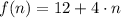B) The 11th term of the sequence is 62.

Explanation:

A) Let
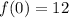`f(0) = 12`, we notice that sequence observes an arithmetic progression, in which there is a difference of 4 between two consecutive elements. The formula for arithmetic progression is:

`f(n) = f(0) +r\cdot n` (1)

Where:

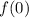`f(0)` - First value of the sequence, dimensionless.

`r` - Arithmetic increase rate, dimensionless.

`n` - Term of the value in the sequence, dimensionless.

If we know that
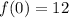`f(0) = 12` and
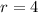`r = 4`, then the explicit formula for the sequence is:

`f(n) = 12+4\cdot n`,
`n \in \mathbb{N}_(O)`

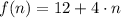B) If we know that
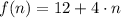`f(n) = 12+4\cdot n` and
`n = 10`, the 11th term of the sequence is:

`f(10) = 12+4\cdot (10)`

`f(10) = 62`

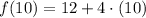
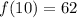
The 11th term of the sequence is 62.

Answer 2

`T_n = 8+ 4n`

`T_(11) = 52`

Explanation:

Given

`Sequence: 12, 16, 20, 24`

Solving (a): Write a formula

The above sequence shows an arithmetic progression

Hence:

The formula can be calculated using:

`T_n = a + (n - 1) d`

In this case:

`a = First\ Term = 12`

Difference (d) is difference of 2 successive terms

So:

`d = 16 - 12 = 20 - 16 = 24 - 20`

`d = 4`

Substitute 4 for d and 12 for a in
`T_n = a + (n - 1) d`

`T_n = 12 + (n - 1) * 4`

Open Bracket

`T_n = 12 + 4n - 4`

Collect Like Terms

`T_n = 12 - 4+ 4n`

`T_n = 8+ 4n`

Hence, the explicit formula is:
`T_n = 8+ 4n`

Solving (b): 11th term

This implies that n = 11

Substitute 11 for n in:
`T_n = 8+ 4n`

`T_(11) = 8+ 4 * 11`

`T_(11) = 8+ 44`

`T_(11) = 52`