Question

Standing on the edge of a​ cliff, Fernando throws a rock upward from a height 512 feet above the water at a speed of 64 feet per second. How long will it take for the rock to land in the​ water?

Answer 1

Answer: 7.6875 seconds.

Explanation:

Let's writhe the motion equations for the rock.

The only force acting on the rock will be the gravitational force, then the acceleration of the rock will be the gravitational acceleration g ≈ 32 ft/s^2

A(t) = -32ft/s^2

Where we have a negative sign because this acceleration pulls the rock downwards.

For the velocity, we must integrate over time, and the constant of integration will be equal to the initial velocity of the rock = 64 ft/s, then the velocity equation is:

V(t) = (-32ft/s^2)*t + 64m/s

For the position, we integrate again over time, and this time the constant of integration will be the initial position, 512ft (Then the water level is at 0 ft)

P(t) = (1/2)*(-32ft/s^2)*t^2 + 64m/s*t + 512 ft

Now we want to find the value of t, the time, such that the rock hits the water.

The rock will land in the water when P(t) = 0ft, becuse we defined the zero in the position as the water.

Then we must solve:

P(t) = 0ft = (1/2)*(-32ft/s^2)*t^2 + 64m/s*t + 512 ft

for t, let's solve this:

0ft = (-16ft/s^2)*t^2 + 64m/s*t + 512 ft

This is a quadratic equation. the two solutions can be found by using the Bhaskara equation, then the solutions will be:

`t = ( -64ft/s +- √((64ft/s)^2 - 4*(-16ft/s^2)*512ft) )/(2*(-16ft/s^2)) = (-64ft/s +- 192ft/s)/(-32ft/s)`

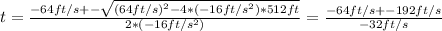
Then the two solutions are:

t = (-64ft/s + 192ft/s)/(-32ft/s^2) = -4s (This time is negative, which is no really defined for this problem, so we can discard this solution)

The other solution is:

t = (-64ft/s - 192ft/s)/(-32ft/s^2) = 7.6875 s

This solution makes sense with the problem, then the answer is 7.6875 seconds.