Question

Please help me no one answers my last few questions
#6

Answer 1

`[f(x)]^2-g(x) = 5x^2-13x-8`

Explanation:

Given

`f(x) = 2x-2\\g(x) = -x^2+5x+12`

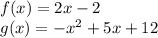
To find:
`[f(x)]^2-g(x)`

First of all the square of first function f(x) will be found and then second function g(x) will be subtracted from the square of first function

Squaring the first function

`[f(x)]^2 = (2x-2)^2\\Using\ (a-b)^2 = a^2-2ab+b^2\\\[f(x)]^2 = (2x)^2-2(2x)(2)+(2)^2\\= 4x^2-8x+4`

Now subtracting g(x) from [f(x)]^2

`[f(x)]^2-g(x) = (4x^2-8x+4)-(-x^2+5x+12)\\\[f(x)]^2-g(x) = 4x^2-8x+4+x^2-5x-12`

Combining alike terms

`[f(x)]^2-g(x) = 4x^2+x^2-5x-8x+4-12\\\[f(x)]^2-g(x) = 5x^2-13x-8`

Hence,

Subtracting g(x) from the square of f(x) gives us:

`[f(x)]^2-g(x) = 5x^2-13x-8`