Question

Two speeding lead bullets, one of mass 15.0 g moving to the right at 295 m/s and one of mass 7.75 g moving to the left at 375 m/s, collide head-on, and all the material sticks together. Both bullets are originally at temperature 30.0°C. Assume the change in kinetic energy of the system appears entirely as increased internal energy. We would like to determine the temperature and phase of the bullets after the collision. (Lead has a specific heat of 128 J/(kg K), a melting point of 327.3°C, and a latent heat of fusion of 2.45 104 J/kg.)

Answer 1

The final temperature of the bullets is 327.3 ºC.

Step-by-step explanation:

Let suppose that a phase change does not occur during collision and collided bullets stop at the end. We represent the phenomenon by the First Law of Thermodynamics:

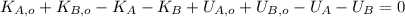`K_(A, o) + K_(B, o)-K_(A)-K_(B)+U_(A,o) + U_(B,o)-U_(A)-U_(B) = 0` (1)

Where:

`K_(A,o)`,
`K_(A)` - Initial and final translational kinetic energies of the 15-g bullet, measured in joules.

`K_(B,o)`,
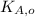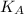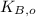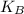`K_(B)` - Initial and final translational kinetic energies of the 7.75-g bullet, measured in joules.

`U_(A,o)`,
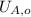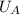`U_(A)` - Initial and final internal energies of the 15-g bullet, measured in joules.

`U_(B,o)`,
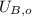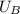`U_(B)` - Initial and final internal energies of the 7.75-g bullet, measured in joules.

By definitions of translational kinetic energy and sensible heat we expand and simplify the equation above:

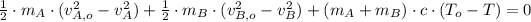`(1)/(2)\cdot m_(A)\cdot (v_(A,o)^(2)-v_(A)^(2))+ (1)/(2)\cdot m_(B)\cdot (v_(B,o)^(2)-v_(B)^(2))+(m_(A)+m_(B))\cdot c\cdot (T_(o)-T) = 0` (2)

Where:

`m_(A)`,
`m_(B)` - Masses of the 15-g and 7.75-g bullets, measured in kilograms.

`v_(A,o)`,
`v_(A)` - Initial and final speeds of the 15-g bullet, measured in meters per second.

`v_(B,o)`,
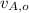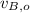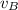`v_(B)` - Initial and final speeds of the 7.75-g bullet, measured in meters per second.

`c` - Specific heat of lead, measured in joules per kilogram-Celsius degree.

`T_(o)`,
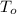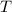`T` - Initial and final temperatures of the bullets, measured in Celsius degree.

Now we clear the final temperature of the bullets:

`(m_(A)+m_(B))\cdot c \cdot (T-T_(o)) = (1)/(2)\cdot [m_(A)\cdot (v_(A,o)^(2)-v_(A)^(2))+m_(B)\cdot (v_(B,o)^(2)-v_(B)^(2))]`

`T-T_(o) = (m_(A)\cdot (v_(A,o)^(2)-v_(A)^(2))+m_(B)\cdot (v_(B,o)^(2)-v_(B)^(2)))/((m_(A)+m_(B))\cdot c)`

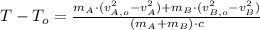
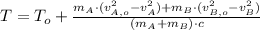`T= T_(o)+(m_(A)\cdot (v_(A,o)^(2)-v_(A)^(2))+m_(B)\cdot (v_(B,o)^(2)-v_(B)^(2)))/((m_(A)+m_(B))\cdot c)` (3)

If we know that
`T_(o) = 30\,^(\circ)C`,
`m_(A) = 15* 10^(-3)\,kg`,
`m_(B) = 7.75* 10^(-3)\,kg`,
`v_(A,o) = 295\,(m)/(s)`,
`v_(B,o) = 375\,(m)/(s)`,
`v_(A) = 0\,(m)/(s)`,
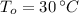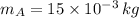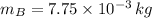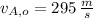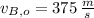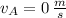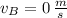`v_(B) = 0\,(m)/(s)` and
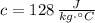`c = 128\,(J)/(kg\cdot ^(\circ)C)`, then the final temperature of the collided bullets is:

`T = 30\,^(\circ)C+((15* 10^(-3)\,kg)\cdot \left[\left(295\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right]+(7.75* 10^(-3)\,kg)\cdot \left[\left(375\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right])/((15* 10^(-3)\,kg+7.75* 10^(-3)\,kg)\cdot \left(128\,(J)/(kg\cdot ^(\circ)C) \right))`

`T = 852.534\,^(\circ)C`

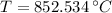
Given that found temperature is greater than melting point, then we conclude that supposition was false. If we add the component of latent heat of fussion, then the resulting equation is:

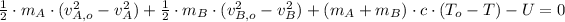`(1)/(2)\cdot m_(A)\cdot (v_(A,o)^(2)-v_(A)^(2))+ (1)/(2)\cdot m_(B)\cdot (v_(B,o)^(2)-v_(B)^(2))+(m_(A)+m_(B))\cdot c\cdot (T_(o)-T)-U = 0` (4)

`U=(1)/(2)\cdot m_(A)\cdot (v_(A,o)^(2)-v_(A)^(2))+ (1)/(2)\cdot m_(B)\cdot (v_(B,o)^(2)-v_(B)^(2))+(m_(A)+m_(B))\cdot c\cdot (T_(o)-T)`

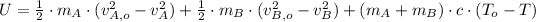
If we know that
`T_(o) = 30\,^(\circ)C`,
`T = 327.3\,^(\circ)C`,
`m_(A) = 15* 10^(-3)\,kg`,
`m_(B) = 7.75* 10^(-3)\,kg`,
`v_(A,o) = 295\,(m)/(s)`,
`v_(B,o) = 375\,(m)/(s)`,
`v_(A) = 0\,(m)/(s)`,
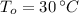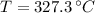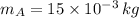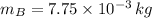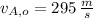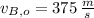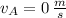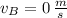`v_(B) = 0\,(m)/(s)` and
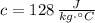`c = 128\,(J)/(kg\cdot ^(\circ)C)`, then latent heat received by the bullets during impact is:

`U =(1)/(2)\cdot (15* 10^(-3)\,kg)\cdot \left[\left(295\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right] + (1)/(2)\cdot (7.75* 10^(-3)\,kg)\cdot \left[\left(375\,(m)/(s) \right)^(2)-\left(0\,(m)/(s) \right)^(2)\right]+(15* 10^(-3)\,kg+7.75* 10^(-3)\,kg)\cdot \left(128\,(J)/(kg\cdot ^(\circ)C) \right) \cdot (30\,^(\circ)C-327.3\,^(\circ)C)`
`U = 331.872\,J`

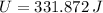
The maximum possible latent heat (
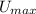`U_(max)`), measured in joules, that both bullets can receive during collision is:

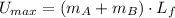`U_(max) = (m_(A)+m_(B))\cdot L_(f)` (5)

Where
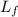`L_(f)` is the latent heat of fusion of lead, measured in joules per kilogram.

If we know that
`m_(A) = 15* 10^(-3)\,kg`,
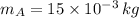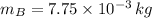`m_(B) = 7.75* 10^(-3)\,kg` and
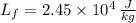`L_(f) = 2.45* 10^(4)\,(J)/(kg)`, then the maximum possible latent heat is:

`U_(max) = (15* 10^(-3)\,kg+7.75* 10^(-3)\,kg)\cdot \left(2.45* 10^(4)\,(J)/(kg) \right)`

`U_(max) = 557.375\,J`

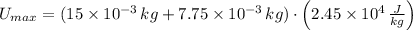
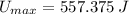
Given that
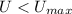`U < U_(max)`, the final temperature of the bullets is 327.3 ºC.