Question

What is the y-intercept of (5,8) and (12,36)

Answer 1

(0, -12)

Explanation:

In order to find the y-intercept of the equation y = mx + b ( where m is the slope and b is the y-intercept), we first have to find the slope. We can do this by using the two points given to us.

To find the slope:

The slope is equal to:
`(y2 - y1)/(x2 - x1)`

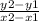
Let's plug (5,8) and (12,36) into the equation:

`(36 - 8)/(12 - 5)`

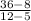
Now let's solve for the slope:

36 -8 = 28

12 - 5 = 7

So we get:
`(28)/(7)`

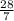
Now that we've found the value of the slope, we can put it into the equation:

y =
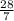`(28)/(7)`x + b

To find the value of b, we can input the values of one of the given points into the equation and solve for b. Let's use (5,8):

Input the values of x and y into the equation: 8 =
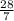`(28)/(7)`(5) + b

Multiple
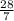`(28)/(7)` by 5: 8 =
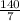`(140)/(7)` + b

Divide 140 by 7: 8 = 20 + b

Subtract 20 from both sides of the equation to isolate b:

8 - 20 = 20 - 20 + b

-12 = b

The y-intercept is (0, -12).

Answer 2

The y intercept is (0,-12)

Explanation:

You use the slope formula and the slope-intercept form to find the slope m and then the y intercept b.