Answer:
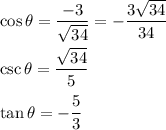
Explanation:
Accorded to trigonometric formula, we know that:
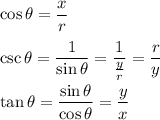
We know what x and y are but not yet knowing what r is. We can find r (radius) using the formula:
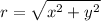
Input x = -3 and y = 5 in.
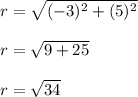
Hence, radius is √34 and we know all we need now. Substitute x = -3, y = 5 and r = √34 in respective areas.
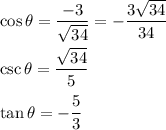
These are the answers to your question. Please let me know if you have any questions regarding my answer or explanation!