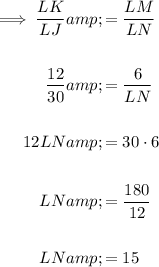Question

If JL = 30, JK = 18, and LM = 6, then the value of LN is:

Answer 1

LN = 15

Explanation:

The arrows on the line segments indicate they are parallel.

`\implies \overline{KM} \parallel \overline{JN}`

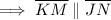
Triangle Proportionality Theorem

If a line parallel to one side of a triangle intersects the other two sides of the triangle, then it divides these two sides proportionally.

`\textsf{If }\overline{KM} \parallel \overline{JN}, \textsf{ then }(LK)/(LJ)=(LM)/(LN)`

Given:

• LM = 6
• JL = 30
• JK = 18

⇒ LK = JL - JK = 30 - 18 = 12

Substituting the values into the equation and solving for LN:

`\begin{aligned}\implies (LK)/(LJ) & = (LM)/(LN)\\\\(12)/(30) & = (6)/(LN)\\\\12LN & = 30 \cdot 6\\\\LN & = (180)/(12)\\\\LN & = 15\end{aligned}`

Answer 2

Answer: LN = 15

Make a proportional relationship:

`\sf (LN)/(JL) = (LM)/(KL)`

Insert the values:

`\rightarrow \sf (LN)/(30) = (6)/(30-18)`

cross multiply:

`\rightarrow \sf LN = (30(6))/(12)`

Simplify:

• 
  `\sf LN =15`