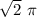Question

Use spherical coordinates. Find the volume of the solid that lies within the sphere x^2 + y^2 + z^2 = 81, above the xy-plane, and below the cone z = x^2 + y^2.

Answer 1

The volume of the solid is 243
`√(2) \ \pi`

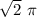
Explanation:

From the information given:

BY applying sphere coordinates:

0 ≤ x² + y² + z² ≤ 81

0 ≤ ρ² ≤ 81

0 ≤ ρ ≤ 9

The intersection that takes place in the sphere and the cone is:

`x^2 +y^2 ( √(x^2 +y^2 ))^2 = 81`

`2(x^2 + y^2) =81`

`x^2 +y^2 = (81)/(2)`

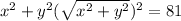
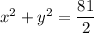
Thus; the region bounded is: 0 ≤ θ ≤ 2π

This implies that:

`z = √(x^2+y^2)`

ρcosФ = ρsinФ

tanФ = 1

Ф = π/4

Similarly; in the X-Y plane;

z = 0

ρcosФ = 0

cosФ = 0

Ф = π/2

So here;
`(\pi)/(4) \leq \phi \le (\pi)/(2)`

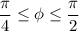
Thus, volume:
`V = \iiint_E \ d V = \int \limits^(\pi/2)_(\pi/4) \int \limits ^(2\pi)_(0) \int \limits^9_0 \rho ^2 \ sin \phi \ d\rho \ d \theta \ d \phi`

`V = \int \limits^(\pi/2)_(\pi/4) \ sin \phi \ d \phi \int \limits ^(2\pi)_(0) d \theta \int \limits^9_0 \rho ^2 d\rho`

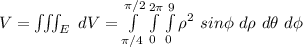
`V = \bigg [-cos \phi \bigg]^(\pi/2)_(\pi/4) \bigg [\theta \bigg]^(2 \pi)_(0) \bigg [(\rho^3)/(3) \bigg ]^(9)_(0)`

`V = [ -0+ (1)/(√(2))][2 \pi -0] [(9^3)/(3)- 0 ]`

V = 243
`√(2) \ \pi`