Answer:
Ambos recipientes tienen la misma densidad, es decir, 10 kilogramos por metros cúbicos.
Explanation:
Recordamos que la densidad de un material uniforme (
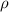 ), medido en kilogramos por metro cúbico, está definido por:
), medido en kilogramos por metro cúbico, está definido por:
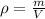 (1)
(1)
Donde:
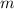 - Masa, medido en kilogramos.
- Masa, medido en kilogramos.
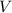 - Volumen, medido en metros cúbicos.
- Volumen, medido en metros cúbicos.
Ahora calculamos la densidad de cada recipiente:
Recipiente A (
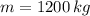 ,
,
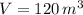 )
)
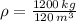
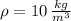
El recipiente A tiene una densidad de 10 kilogramos por metro cúbico.
Recipiente B (
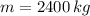 ,
,
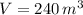 )
)
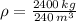
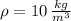
El recipiente B tiene una densidad de 10 kilogramos por metro cúbico.
Ambos recipientes tienen la misma densidad, es decir, 10 kilogramos por metros cúbicos.