Question

Find the volume of the figure. Round your answer to the nearest tenth if necessary. Use 3.14 for T.

A cylinder has a radius of 7 meters and a height of 3 meters.
The volume of the cylinder is approximately
m³.

Answer 1

`\boxed{ \rm \: Volume_((Cylinder)) \approx \: 461.6 \: {m}^(3) } \rm (rounded \: to \: nearest \: tenth)`

Explanation:

Given dimensions:

• Radius of the cylinder = 7 metres
• Height of the cylinder = 3 metres

Given value of π :

• π = 3.14

To find:

• The Volume of the cylinder

Solution:

Here, we'll need to use the formulae of the volume of cylinder,to find it's volume.Its actually like a savior while solving these type of questions.

`\pink{\star}\boxed{\rm \: Volume_((Cylinder)) = \pi{r} {}^(2) h}\pink{\star}`

where,

• π = 3.14
• r² = (radius)²
• h = height

Plug/substitute them onto the formulae,then simplify it using PEMDAS.

• [We'll substitute the value of π later]

`\rm \: Volume_((Cylinder)) = \pi(7) {}^(2) * 3`

`\rm \: Volume_((Cylinder)) = \pi(49)(3)`

`\rm \: Volume_((Cylinder)) = 147\pi \:`

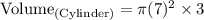
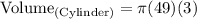
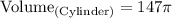
• Now substitute the value of π.

`\rm \: Volume_((Cylinder)) = 147 * 3.14`

`\rm \: Volume_((Cylinder)) = 461.58 \: {m}^(3)`

`\boxed{\rm \: Volume_((Cylinder)) \approx \: 461.6 \: {m}^(3)} \rm (rounded \: to \: nearest \: tenth) \:`

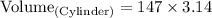
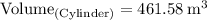
Hence, we can conclude that:

The volume of the cylinder is approximately

461.6 m³.

`\rule{225pt}{2pt}`