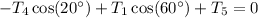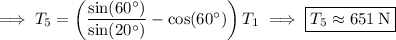Question

Find the tension in the ropes shown in the figure if the supported object weighs 600N.

Answer 1

By Newton's second and third laws, we have the following net forces at

• point A:

`\sum F_x = -T_1 \cos(60^\circ) + T_2 \cos(60^\circ) = 0`

`\sum F_y = T_1 \sin(60^\circ) + T_2 \sin(60^\circ) - 600 \,\mathrm N = 0`

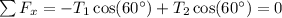
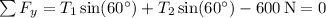
Together, these equations tell us
`\boxed{T_1=T_2\approx 346 \,\mathrm N}`.

• point B:

`\sum F_x = T_3 \cos(20^\circ) - T_2 \cos(60^\circ) - T_5 = 0`

`\sum F_y = T_3 \sin(20^\circ) - T_2 \sin(60^\circ) = 0`

• point C:

`\sum F_x = -T_4 \cos(20^\circ) + T_1 \cos(60^\circ) + T_5 = 0`

`\sum F_y = T_4 \cos(20^\circ) - T_1 \sin(60^\circ) = 0`

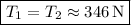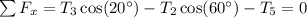
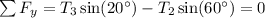
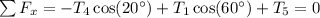
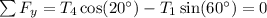
Combining the horizontal force equations for points B and C and using the fact that
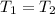`T_1=T_2` gives

`(T_3 \cos(20^\circ) - T_2 \cos(60^\circ) - T_5) + (-T_4  \cos(20^\circ) + T_1 \cos(60^\circ) + T_5) = 0 + 0`

`\implies (T_3 - T_4) \cos(20^\circ) = 0 \implies T_3=T_4`

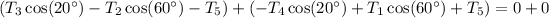
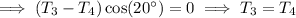
Then combining the vertical force equations for B and C, we find

`(T_3 \sin(20^\circ) - T_2 \sin(60^\circ)) + (T_4 \sin(20^\circ) - T_1 \sin(60^\circ)) = 0 + 0`

`\implies 2 T_3 \sin(20^\circ) - 2 T_1 \sin(60^\circ) \implies T_3 = (\sin(60^\circ))/(\sin(20^\circ)) T_1`

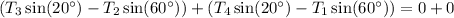
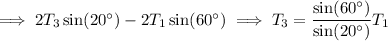
so that
`\boxed{T_3 = T_4 \approx 877 \,\mathrm N}`

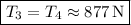
Lastly solve for
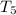`T_5` using either horizontal force equation for B or C.

`-T_4 \cos(20^\circ) + T_1 \cos(60^\circ) + T_5 = 0`

`\implies T_5 = \left((\sin(60^\circ))/(\sin(20^\circ)) - \cos(60^\circ)\right) T_1 \implies \boxed{T_5 \approx 651\,\mathrm N}`