Answer:
162 metres
Explanation:
Since h is proportional to the square of v, we know that their ratio must be constant, so
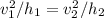 where v1 and v2 are velocities and h1 and h2 are their respective heights.
where v1 and v2 are velocities and h1 and h2 are their respective heights.
Since we are given that v = 10 and h = 8, we can set v1 = 10 and h1 = 8 and since we are trying to find the height for v = 45, we can set v2 = 45. Inputting these values into the equation and solving, we get
10^2/8 = 45^2/h2
h2 = 45^2/(10^2/8) = 162 metres
I hope this helps!