Question

Find the deposit required to accumulate $7700 after investing 3 years in an account that pays an APR of 5% compounded quarterly. How much is earned in interest?

Answer 1

The deposit required is $6633.62 and the interest earned is $366.38

Explanation:

Compound interest occurs when the interest earned is reinvested rather than paying it out. When it happens interest in the next period is then earned on the principal sum plus previously accumulated interest.

The formula is:

`{\displaystyle A=P\left(1+{\frac {r}{n}}\right)^(nt)}`

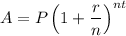
Where:

A = final amount

P = initial principal balance

r = interest rate

n = number of times interest applied per time period

t = number of time periods elapsed

It's given the final amount A=$7700 after t=3 years of investment in an account that pays an APR of r=5%=0.05. Since the interests compound quarterly and there are 4 quarters in a year, then n=4.

To find the principal P, we solve the previous equation for P as follows:

`{\displaystyle P=A\left(1+{\frac {r}{n}}\right)^(-nt)}`

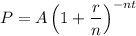
Substituting:

`{\displaystyle P=7700\left(1+{\frac {0.05}{4}}\right)^(-4\cdot 3)}`

`{\displaystyle P=7700\left(1+0.0125}\right)^(-12)}`

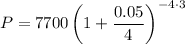
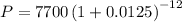
P=$6633.62

The interest earned is:

I = A - P = $7700 - $6633.62 = $366.38

The deposit required is $6633.62 and the interest earned is $366.38