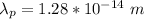Question

Calculate the de Broglie wavelength of: a) A person running across the room (assume 180 kg at 1 m/s) b) A 5.0 MeV proton

Answer 1

a

`\lambda = 3.68 *10^(-36) \ m`

b

`\lambda_p = 1.28*10^(-14) \ m`

Step-by-step explanation:

From the question we are told that

The mass of the person is
`m = 180 \ kg`

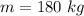
The speed of the person is
`v = 1 \ m/s`

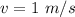
The energy of the proton is
`E_ p = 5 MeV = 5 *10^(6) eV = 5.0 *10^6 * 1.60 *10^(-19) = 8.0 *10^(-13) \ J`

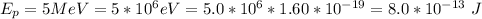
Generally the de Broglie wavelength is mathematically represented as

`\lambda = (h)/(m * v )`

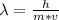
Here h is the Planck constant with the value

`h = 6.62607015 * 10^(-34) J \cdot s`

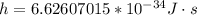
So

`\lambda = (6.62607015 * 10^(-34))/( 180 * 1 )`

=>
`\lambda = 3.68 *10^(-36) \ m`

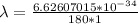
Generally the energy of the proton is mathematically represented as

`E_p = (1)/(2) * m_p * v^2_p`

Here
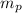`m_p` is the mass of proton with value
`m_p = 1.67 *10^(-27) \ kg`

=>
`8.0*10^(-13) = (1)/(2) * 1.67 *10^(-27) * v^2`

=>
`v _p= \sqrt{(8.0 *10^(-13))/( 0.5 * 1.67 *10^(-27)) }`

=>
`v = 3.09529 *10^(7) \ m/s`

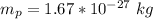
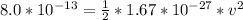
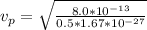
So

`\lambda_p = (h)/(m_p * v_p )`

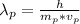
so
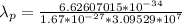
`\lambda_p = (6.62607015 * 10^(-34))/(1.67 *10^(-27) * 3.09529 *10^(7) )`

=>
`\lambda_p = 1.28*10^(-14) \ m`