Question

The altitude of a triangle is increasing at a rate of 1 cm/min while the area of the triangle is increasing at a rate of 2 cm^2/min. At what rate is the base of the triangle changing when the altitude is 10 cm and the area is 120 cm^2?

Answer 1

The base is decreasing at 2 cm/min.

Explanation:

The area (A) of a triangle is given by:

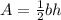`A = (1)/(2)bh` (1)

Where:

b: is the base

h: is the altitude = 10 cm

If we take the derivative of equation (1) as a function of time we have:

`(dA)/(dt) = (1)/(2)((db)/(dt)h + (dh)/(dt)b)`

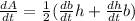
We can find the base by solving equation (1) for b:

`b = (2A)/(h) = (2*120 cm^(2))/(10 cm) = 24 cm`

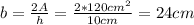
Now, having that dh/dt = 1 cm/min, dA/dt = 2 cm²/min we can find db/dt:

`2 cm^(2)/min = (1)/(2)((db)/(dt)*10 cm + 1 cm/min*24 cm)`

`(db)/(dt) = (2*2 cm^(2)/min - 1 cm/min*24 cm)/(10 cm) = -2 cm/min`

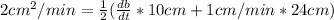
Therefore, the base is decreasing at 2 cm/min.

I hope it helps you!