Answer:
a) The kinetic energy of the particle at any time t is
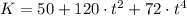 .
.
b) The acceleration of the particle at time t is
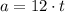 . The force acting on the particle at time t is
. The force acting on the particle at time t is
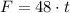 .
.
c) The power being delivered to the particle at time t is
 .
.
d) The work done on the particle in the interval t = 0 to t = 5 is 48000 joules.
Step-by-step explanation:
a) The kinetic energy of the particle is entirely translational, whose formula is:
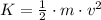 (1)
(1)
Where:
 - Translational kinetic energy, measured in joules.
- Translational kinetic energy, measured in joules.
 - Mass of the particle, measured in kilograms.
- Mass of the particle, measured in kilograms.
 - Velocity of the particle, measured in meters per second.
- Velocity of the particle, measured in meters per second.
The velocity of the particle is the rate of change of the position of the particle in time, that is:
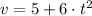 (2)
(2)
Where
 is the time, measured in seconds.
is the time, measured in seconds.
By substituting on (1), we have the following expression: (
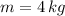 )
)
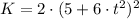

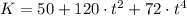
The kinetic energy of the particle at any time t is
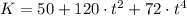 .
.
b) The acceleration of the particle is the rate of change of the velocity of the particle in time, that is:
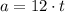 (3)
(3)
Where
 is the acceleration of the particle, measured in meters per square second.
is the acceleration of the particle, measured in meters per square second.
The acceleration of the particle at time t is
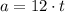 .
.
The force is obtained by multiplying (3) by the mass of the particle. That is to say: (
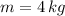 )
)
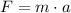 (4)
(4)
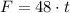
The force acting on the particle at time t is
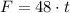 .
.
c) According to the Work-Energy Theorem, the change in kinetic energy of the particle equals the change in the net work done on the particle. In this case, the power is equal to the rate of change in kinetic energy.
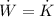 (5)
(5)
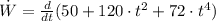

The power being delivered to the particle at time t is
 .
.
d) The work done on the particle (
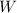 ), measured in joules, is equal to the change of the kinetic energy of the particle:
), measured in joules, is equal to the change of the kinetic energy of the particle:
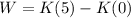 (6)
(6)
![W = [50+120\cdot (5)^(2)+72\cdot (5)^(4)]-[50+120\cdot (0)^(2)+72\cdot (0)^(4)]](https://img.qammunity.org/2021/formulas/physics/college/6vttbz834299o3h308fjv9fzklk9cs6fln.png)
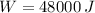
The work done on the particle in the interval t = 0 to t = 5 is 48000 joules.