Answer:
(a) The coordinates of the inflection point are (1; 8) and, being the value of a less than zero, then these coordinates indicate the maximum of the function.
(b) The y-intercept has a value of 6
(c) The coordinates of the x-intercepts have a value of x=3 and x=-1
Explanation:
You know y= -2*(x-1)² + 8
(a) Every quadratic function can be expressed by the canonical form:
f(x)=y= a*( x- h)² + k
where a is the principal coefficient and the ordered pair (h; k) are the coordinates of the vertex of the parabola.
The quadratic function will have a maximum or minimum value at the vertex. If a> 0, the parabola is concave, that is, it will have its branches upwards, therefore the vertex will indicate the minimum of the function. But if a <0 the parabola is convex and the vertex will indicate the maximum of the function.
Comparing the given equation with the canonical form of a quadratic function you can see that:
Then, the coordinates of the inflection point are (1; 8) and, being the value of a less than zero, then these coordinates indicate the maximum of the function.
(b) The y-intercept arises from evaluating the function at x = 0. So, in this case:
y= -2*(0-1)² + 8
Solving:
y= -2*(-1)² + 8
y= -2*1 + 8
y= -2+8
y= 6
The y-intercept has a value of 6
(c) The roots or coordinates of the x-intercepts arise from evaluating the function at y = 0. So, in this case:
0= -2*(x-1)² + 8
Solving:
-8= -2*(x-1)²
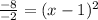
4= (x-1)²
√4= |x-1|
⇒ 2=x-1 → 2+1=x → 3=x
⇒ -2=x-1 → -2+1=x → -1=x
The coordinates of the x-intercepts have a value of x=3 and x=-1