Question

The vertices of her garden are located at the points (−1,5), (4,2) and (9,−4) on a coordinate grid. If each unit on the grid represents a foot and the material costs $8 per foot, how much will she pay for the material on the side between points (−1,5) and (4,2)?

Answer 1

Given:

The vertices of the garden on a coordinate grid are (−1,5), (4,2) and (9,−4).

Each unit on the grid represents a foot and the material costs $8 per foot.

To find:

The cost for the material on the side between points (−1,5) and (4,2).

Solution:

Distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

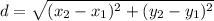
Using the above formula, the distance between points (−1,5) and (4,2) is

`d=√((4-(-1))^2+(2-5)^2)`

`d=√((4+1)^2+(-3)^2)`

`d=√((5)^2+(-3)^2)`

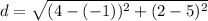
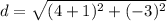
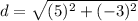
On further simplification, we get

`d=√(25+9)`

`d=√(34)`

`d\approx 5.83`

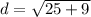
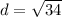
Now,

1 unit = 1 foot and 1 foot material costs is $8.

So, 1 unit material cost is $8.

Cost of material for 5.83 units is

`5.83* 8=46.64`

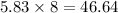
Therefore, the cost for the material on the side between points (−1,5) and (4,2) is $46.64.