Question

Assuming the frequency stays the same, will a sound wave have a larger or smaller wavelength when it passes from room temperature air (20°C) to water? Explain your answer with math, words, or both.​

Answer 1

The wavelength of this sound wave would be longer in water than in the air.

Step-by-step explanation:

Let
`f` denote the frequency of this sound wave (standard unit:
`\rm s^(-1)`.)

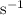If the speed of sound in a particular medium is
`v` (standard unit:
`{\rm m \cdot s^(-1)}`,) the wavelength
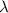`\lambda` of this wave in that medium would be:

`\begin{aligned} \lambda = (v)/(f) && \genfrac{}{}{0}{}{(\text{standard unit: ${\rm m \cdot s^(-1)}$})}{(\text{standard unit: ${\rm s^(-1)}$})}\end{aligned}`.

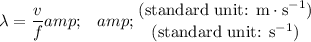Let
`v_\text{water}` denote the speed of sound in water and let
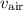`v_\text{air}` denote the speed of sound in the air at room temperature.

The wavelength of this sound wave in water would be:

`\displaystyle \lambda_{\text{water}} = \frac{v_{\text{water}}}{f}`.

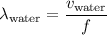The wavelength of this sound wave in the air at room temperature would be:

`\displaystyle \lambda_{\text{air}} = \frac{v_{\text{air}}}{f}`.

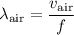Fact: the speed of sound in water (a liquid) is greater than the speed of sound in air at room temperature. In other words:

`v_{\text{water}} > v_{\text{air}}`.

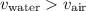Given that
`f > 0`:

`\begin{aligned} \frac{v_{\text{water}}}{f} > \frac{v_{\text{air}}}{f}\end{aligned}`.

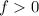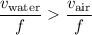Therefore:

`\begin{aligned} \lambda_{\text{water}} > \lambda_{\text{air}}\end{aligned}`.