Answer:
0.0384
Explanation:
Given a fair 5 sided die rolled 5 times.
Numbers on it are 1, 2, 3, 4, 5.
To find:
The probability that each number will occur exactly once.
Solution:
Formula for probability of an event E:
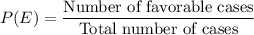
At the first roll of die, any number can occur.
So number of possible outcomes = 5
Total number of possible outcomes = 5
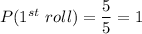
At the second roll of die, any number can occur other than that occurred in first roll.
So number of possible outcomes = 4
Total number of possible outcomes = 5
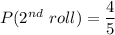
At the third roll of die, any number can occur other than that occurred in first and second roll.
So number of possible outcomes = 3
Total number of possible outcomes = 5
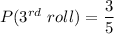
At the fourth roll of die, any number can occur other than that occurred in first, second and third roll.
So number of possible outcomes = 2
Total number of possible outcomes = 5
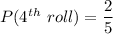
At the fifth roll of die, any number can occur other than that occurred in first, second, third and fourth roll.
So number of possible outcomes = 1
Total number of possible outcomes = 5
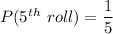
The required probability will be multiplication of all the five probabilities.
