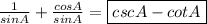Hi there!
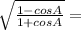
We can begin by multiplying by its conjugate:
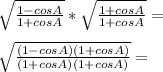
Simplify using the identity:
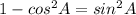
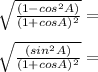
Take the square root of the expression:
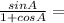
Multiply again by the conjugate to get a SINGLE term in the denominator:
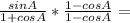
Simplify:
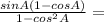
Use the above trig identity one more:
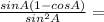
Cancel out sinA:
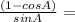
Split the fraction into two:
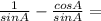
Recall:
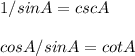
Simplify: