Question

A sample of the lava flow within the outcrop has 707 Uranium-235 atoms, and 293 Lead-207 atoms. How old is the lava flow?

Answer 1

The lava flow is approximately 351.925 million years.

Step-by-step explanation:

We find that atoms of Uranium-235 decays and turns into Lead-207 and that half-life of the former one is
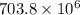`703.8* 10^(6)` years. The initial amount of Uranium-235 is the sum of current atoms of Uranium-235 and Lead-207. The decay of isotopes is modelled by the following ordinary differential equation:

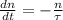`(dn)/(dt) = -(n)/(\tau)` (Eq. 1)

Where:

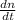`(dn)/(dt)` - Rate of change of the amount of Uranium-235 atoms, measured in atoms per year.

`n` - Current amount of Uranium-235 atoms, measured in atoms.

`\tau` - Time constant, measured in years.

The solution of this differential equation is described below:

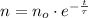`n = n_(o)\cdot e^{-(t)/(\tau) }` (Eq. 2)

Where:

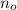`n_(o)` - Initial amount of Uranium-235 atoms, measured in atoms.

`t` - Time, measured in years.

In addition, we can calculate the time constant in terms of the half-life:

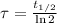`\tau = (t_(1/2))/(\ln 2)` (Eq. 3)

If we know that
`n_(o) = 1000\,atoms`,
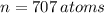`n = 707\,atoms` and
`t_(1/2) = 703.8* 10^(6)\,yr`, then the age of the lava flow is:

From (Eq. 2):

`t = -\tau \cdot \ln (n)/(n_(o))`

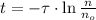
By (Eq. 3);

`\tau = (703.8* 10^(6)\,yr)/(\ln 2)`

`\tau \approx 1.015* 10^(9)\,yr`

`t = -(1.015* 10^(9))\cdot \ln (707\,atoms)/(1000\,atoms)`

`t \approx 351.925* 10^(6)\,yr`

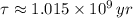
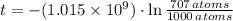
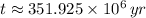
The lava flow is approximately 351.925 million years.