Question

The length of one side of a rectangle is 12 units longer than the length of another side. The rectangle's area is 220 square units. What is the length, in units, of the shorter of these two sides?

Answer 1

Length of the shorter side = -10 units or 22 units.

Step-by-step explanation:

Let x = length of the longer side of the rectangle

Let y = length (width or breadth) of the shorter side of the rectangle

Given the following data;

x = y + 12

Area = 220 units

We know that the area of a rectangle is given by the formula;

`Area, A = length * width`

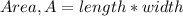
Substituting into the equation, we have;

`220 = (y + 12) * y`

`220 = y^(2) + 12y`

Rearranging the equation, we have;

`y^(2) + 12y - 220 = 0`

Solving the quadratic equation by factorization, we have;

Factors are = -10 and 22

`y^(2) - 10y + 22y - 220 = 0`

`y(y - 10) + 22(y - 10) = 0`

`(y - 10)(y + 22) = 0`

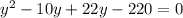
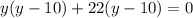
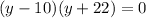
Therefore, y = 10 units or -22 units

To find the value of x;

When y = 10 units

x = y + 12

Substituting into the equation;

x = 10 + 12 = 22

x = 22

When y = -22 units

x = y + 12

Substituting into the equation;

x = -22 + 12 = -10

x = -10

Check;

When x = 22 and y = 10

A = L * W = 22 * 10 = 220 units

When x = -10 and y = -22

A = L * W = -10 * -22 = 220 units