Question

Draw and set up the integrals for the area enclosed by the y–axis, the curve y = (x + 1)1/2 and y = 2. Compute one of them.

Region II only please

Answer 1

If the definitions of type I and type II regions is the same as in the link provided, then as a type I region the integration domain is the set

`R_(\rm I) = \left\{(x,y) \mid 0 \le x \le 3 \text{ and } √(x+1) \le y \le 2\right\}`

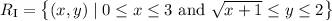
and as a type II region,

`R_(\rm II) = \left\{(x,y) \mid 0 \le x \le y^2-1 \text{ and } 1 \le y \le 2\right\}`

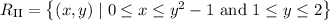
where we solve y = √(x + 1) for x to get x as a function of y.

A. The area of the type I region is

`\displaystyle \iint_{R_(\rm I)} dA = \int_0^3 \int_(√(x+1))^2 dy \, dx = \int_0^3 (2 - √(x+1)) \, dx = \boxed{\frac43}`

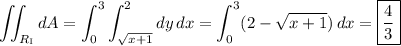
B. The area of the type II region is of course also

`\displaystyle \iint_{R_(\rm II)} dA = \int_1^2 \int_0^(y^2-1) dx \, dy = \int_1^2 (y^2-1) \, dy = \boxed{\frac43}`

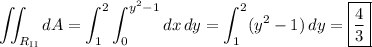
I've attached a plot of the type II region to give an idea of how it was determined. The black arrows indicate the domain of x as it varies from the line x = 0 (y-axis) to the curve y = √(x + 1).