Question

David kicks a ball off the ground. After t seconds, it’s height, h (in feet), is given by the formula h=-16t^2+80t. How many seconds does the ball reach its maximum height? What is the maximum height reached by the ball?

Answer 1

The ball reaches its maximum height at 2.5 seconds

The maximum height is 100 feet

Explanation:

Maximum Value of Functions

We use the derivative of a function to find its maximum or minimum value over a given interval.

Given a function y=f(x), the first derivative criterion establishes if x=a is such that:

f'(a)=0, and f''(a) < 0 then x=a is a maximum of f.

The height h in feet of a ball after t seconds is:

`h(t)=-16t^2+80t`

Find the first derivative:

`h'(t)=-32t+80`

Equate to 0:

`-32t+80=0`

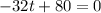
Subtract 80:

`-32t=-80`

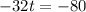
Divide by -32:

`t = -80 / (-32) = 2.5`

t=2.5 seconds

Find the second derivative:

h''(t)=-32

Since h''(t) is always negative, then

The ball reaches its maximum height at 2.5 seconds

To find the value of the maximum height, substitute t=2.5 into the function:

`h(2.5)=-16(2.5)^2+80*2.5=-100+200 = 100`

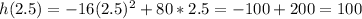
The maximum height is 100 feet