Question

3a: complete the table with values for x and y that makes this equation true 3x+y=15

3b: create a graph, plot these points, and find the slope of the line that goes through them.

Answer 1

a. see the attachment for the table (also reproduced below)

b. slope = -3; see the attachment for a graph

Explanation:

A table of values for the function can be filled a couple of ways. One way is to draw the graph of the equation, and read the point values from it. Another way is to solve for each of the variables, and use those equations to find the missing table values.

__

a.

Solving the equation for y, we get ...

3x +y = 15

y = -3x +15 . . . . . . subtract 3x; this is "point-slope form"

For the purpose of evaluating for different values of x, we can rearrange this a bit to ...

y = 3(5 -x) . . . . factor out 3

The given table has x-values of 0, 2, 3, 6. The corresponding y-values are ...

y = 3(5 -{0, 2, 3, 6}) = 3{5, 3, 2, -1} = {15, 9, 6, -3} . . . . for x={0, 2, 3, 6}

Solving the equation for x, we get ...

y/3 = 5 -x . . . . . divide the above equation by 3

x = 5 -(y/3) . . . . . add x-(y/3)

For y-values {0, 3, 8}, the corresponding x-values are ...

x = 5 -{0, 3, 8}/3 = 5 -{0, 1, 8/3} = {5, 4, 7/3} . . . . for y={0, 3, 8}

Then our table of values is ...

`\begin{array}c\cline{1-8}x&2&4&6&0&3&5&7/3\\y&9&3&-3&15&6&0&8\\\cline{1-8}\end{array}`

__

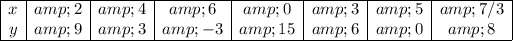
b.

The points in the above table can be plotted, and the line drawn through them. Sometimes using the points that are farthest apart makes this easier: (0, 15) and (6, -3).

slope

When we solved for y, we had the equation in slope-intercept form. The slope is the x-coefficient in that equation:

y = -3x +15 ⇒ slope = -3