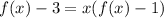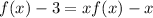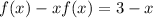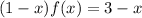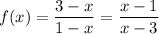I assume by f¹, you actually mean f⁻¹ as in the inverse of f. I also assume you are asked to find f(x) (as in the inverse of f⁻¹) and f⁻¹(4).
Given that
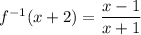
with x ≠ 1, we can find f⁻¹(x) by replacing x + 2 with x :
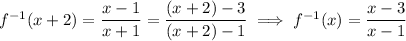
Then when x = 4, we have

Of course, we also could have just substituted x = 2 into the definition of f⁻¹(x + 2) :

To find f(x), we fall back to the definition of an inverse function:
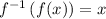
Then by definition of f⁻¹, we have
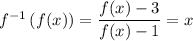
Solve for f :