Question

Please help due NOW PLEASE HELP!!
Will mark as brilliant

Answer 1

Variable

Explanation:

In the given table of values:

• The independent variable (x-value) is the week.
• The dependent variable (y-value) is the number of computer tablets sold.

To determine if the rates of change are constant or variable, we need to calculate the rate of change (slope) between each consecutive pair of (x, y) points. To do this, we can use the slope formula:

`\boxed{\begin{array}{l}\underline{\textsf{Slope formula}}\\\\\large\text{$m=(y_2-y_1)/(x_2-x_1)$}\\\\\textsf{where:}\\\phantom{w}\bullet\;\;m\; \textsf{is the slope.}\\\phantom{w}\bullet\;\;(x_1,y_1)\;\textsf{and}\;(x_2,y_2)\;\textsf{are two points on the line.}\\\\\end{array}}`

The rate of change between weeks 1 and 3 is:

`\textsf{Rate of change (wks 1 - 3)}=(96-32)/(3-1)=(64)/(2)=32\; \textsf{computers sold per week}`

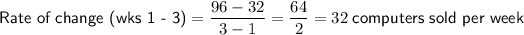
The rate of change between weeks 3 and 4 is:

`\textsf{Rate of change (wks 3 - 4)}=(128-96)/(4-3)=(32)/(1)=32 \;\textsf{computers sold per week}`

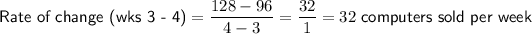
The rate of change between weeks 4 and 8 is:

`\textsf{Rate of change (wks 4 - 8)}=(224-128)/(8-4)=(96)/(4)=24\;\textsf{computers sold per week}`

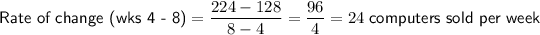
As the rate of change between weeks 4 and 8 is not the same as the rates of change between the other weeks, the rates of change are variable.