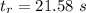Question

The peripheral speed of the tooth of a 10-in.-diameter circular saw blade is 230 ft/s when the power to the saw is turned off. The speed of the tooth decreases at a constant rate, and the blade comes to rest in 17 s. Determine the time at which the total acceleration of the tooth is 130 ft/s2.

Answer 1

The time is
`t_r =21.58 \ s`

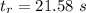
Step-by-step explanation:

From the question we are told that

The diameter of the circular saw is
`d = 10 \ in = (10)/(12) = 0.833 \ feet`

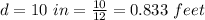
The peripheral speed is
`u = 230 \ ft/s`

The time taken for the blade to come to rest is t = 17 s

The total acceleration of the tooth considered is
`a = 130 \ ft/s^2`

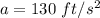
Generally the radius of the blade is mathematically represented as

`r = (0.833)/(2)= 0. 4165 \ feet`

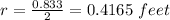
Generally the tangential acceleration of the blade is mathematically represented as

`a__(t)} = (v - u)/(t)`

Here v is the final velocity of the tooth of the blade which is zero since the blade came to rest

so

`a__(t)} = (0 - 230)/( 17)`

=>
`a__(t)} = - 13.53 \ ft/s^2`

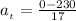
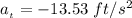
Generally the total acceleration of the tooth of the blade is mathematically represented as

`a = √(a_t^2 + a_r^2)`

Here
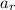`a_r` is the radial acceleration , now making
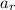`a_r` the subject of the formula we have that

`130= √(13.56 ^2 + a_r^2)`

=>
`a_r = √(130^2 -(- 13.56)^2)`

=>
`a_r = 129.3 \ m/s^2`

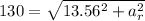
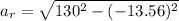
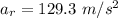
Generally radial acceleration is mathematically represented as

`a_r = (v_r^2)/(r)`

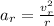
Here
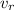`v_r` is the velocity at which the total acceleration is 130 ft/s2.

=>
`v_r = √(a_r * r )`

=>
`v_r = √(129.3 * 0.4165 )`

=>
`v_r = 7.34 \ m/s`

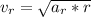
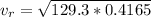
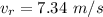
Generally the time at which the total acceleration is 130 ft/s2. is mathematically represented as

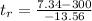
`t_r = (7.34 - 300)/(a_t)`

=>
`t_r = (7.34 - 300)/(-13.56)`

=>
`t_r =21.58 \ s`