Question

A thin spherical shell has a radius of 0.70 m. An applied torque of 860 N m gives the shell an angular acceleration of 4.70 rad/s2 about an axis through the center of the shell. What is the rotational inertia of the shell about the axis of rotation

Answer 1

`I=182.97\ kg-m^2`

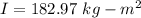
Step-by-step explanation:

Given that,

Radius of a spherical shell, r = 0.7 m

Torque acting on the shell,
`\tau=860\ N`

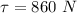
Angular acceleration of the shell,
`\alpha =4.7\ m/s^2`

We need to find the rotational inertia of the shell about the axis of rotation. The relation between the torque and the angular acceleration is given by :

`\tau=I\alpha`

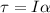
I is the rotational inertia of the shell

`I=(\tau)/(\alpha )\\\\I=(860)/(4.7)\\\\I=182.97\ kg-m^2`

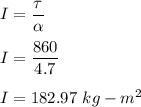
So, the rotational inertia of the shell is
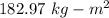`182.97\ kg-m^2`.