Answer:
it lies between 8 hours and 12 hours in a week
Explanation:
Since in the question it is mentioned that the distribution consist of uni-modal, symmetric and bell shaped so here the empirical formual to be used for the mean and the standard deviation
Also the 68% would be fall within one standard deviation above and below the mean
Now
1 standard deviation below the mean is
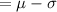
= 10 - 2
= 8 hours
And, above the mean is
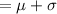
= 10 + 2
= 12 hours
Hence, it lies between 8 hours and 12 hours in a week