Question

What mass in grams of MgSO4 is required to make 59.3 mL of 2.68 M
solution?

Answer 1

Approximately
`19.1\; \rm g`.

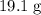Step-by-step explanation:

Number of moles of formula units of magnesium sulfate required to make the solution

The unit of concentration in this question is "
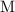`\rm M`". That's equivalent to "
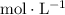`\rm mol \cdot L^(-1)`" (moles per liter.) In other words:

`c(\mathrm{MgSO_4}) = 2.68\; \rm M = 2.68\; \rm mol \cdot L^(-1)`.

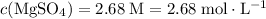However, the unit of the volume of this solution is in milliliters. Convert that unit to liters:

`\displaystyle V = 59.3\; \rm mL = 59.3 \; \rm mL * (1\; \rm L)/(1000\; \rm mL) = 0.0593\; \rm L`.

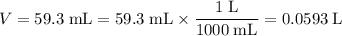Calculate the number of moles of
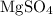`\rm MgSO_4` formula units required to make this solution:

`\begin{aligned}n(\rm MgSO_4) &= c \cdot V \\ &= 2.68 \; \rm mol \cdot L^(-1) * 0.0593\; \rm L \approx 0.159\; \rm mol \end{aligned}`.

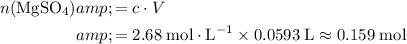Mass of magnesium sulfate in the solution

Look up the relative atomic mass data of
`\rm Mg`,
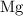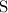`\rm S`, and
`\rm O` on a modern periodic table:

• 
  `\rm Mg`:
  `24.305`.
• 
  `\rm S`:
  `\rm 32.06`.
• 
  `\rm O`:
  `15.999`.

Calculate the formula mass of
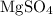`\rm MgSO_4` using these values:

`M(\mathrm{MgSO_4}) = 24.305 + 32.06 + 4 * 15.999 \approx 120.361\; \rm g \cdot mol^(-1)`.

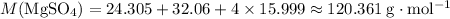Using this formula mass, calculate the mass of that (approximately)
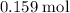`0.159\; \rm mol` of
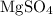`\rm MgSO_4` formula units:

`\begin{aligned}m(\mathrm{MgSO_4}) &= n \cdot M \\&\approx 0.159 \; \rm mol * 120.361 \; \rm g \cdot mol^(-1) \approx 19.1\; \rm g\end{aligned}`.

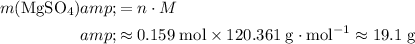Therefore, the mass of
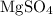`\rm MgSO_4` required to make this solution would be approximately
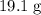`19.1\; \rm g`.