Question

F(x) = (2x²+5)(11x +14)
Find f’’’(x)

Answer 1

`f^(\prime\prime\prime)(x) = 132`.

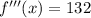Explanation:

Start by expanding the expression of
`f(x)`.

`\begin{aligned} f(x) &= (2\, x^2 + 5) \, (11\, x+ 14) \\ &= 2\, x^2\, (11\, x + 14) + 5\, (11\, x + 14)\\&= \left(22\, x^3 + 28\, x^2\right) + \left(55\, x + 70\right) = 22\, x^3 + 28\, x^2 + 55\, x + 70\end{aligned}`.

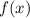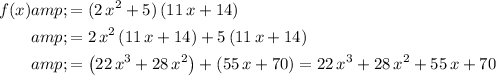The question is asking for the third derivative of that expression:

`\begin{aligned} \frac{d^3}{{d x}^3}\left[22\, x^3 + 28\, x^2 + 55\, x + 70\right]\end{aligned}`.

That's equivalent to finding:

`\begin{aligned} \frac{d^3}{{d x}^3}\left[22\, x^3\right] + \frac{d^3}{{d x}^3} \left[28\, x^2\right] + \frac{d^3}{{d x}^3} \left[55\, x\right] + \frac{d^3}{{d x}^3} \left[70\right]\end{aligned}`.

Move the constants outside of the derivative operator:

`\begin{aligned} 22\, \left(\frac{d^3}{{d x}^3}\left[x^3\right]\right) + 28\, \left(\frac{d^3}{{d x}^3} \left[x^2\right]\right) + 55\, \left(\frac{d^3}{{d x}^3} \left[x\right]\right) + \frac{d^3}{{d x}^3} \left[70\right]\end{aligned}`.

Let
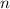`n` denote an integer. By the power rule:

`\displaystyle (d)/(d x) \left[ x^(n)\right] = n\, x^(n-1)`.

Apply these two rules repeatedly to find
`\displaystyle (d^3)/(d x^3)\, \left[ x^3 \right]`,
`\displaystyle (d^3)/(d x^3)\, \left[ x^2 \right]`, and
`\displaystyle (d^3)/(d x^3)\, \left[ x \right]`.

`\displaystyle \frac{d^3}{{d x}^3}\, \left[ x^3 \right] = \frac{d^2}{{d x}^2} \left[3\, x^2\right] = \frac{d}{{d x}} \left[6\, x\right] = 6`.

`\displaystyle \frac{d^3}{{d x}^3}\, \left[ x^2 \right] = \frac{d^2}{{d x}^2} \left[2\, x\right] = \frac{d}{{d x}} \left[ 1 \right] = 0` (the first derivative of a constant is zero.)

`\displaystyle \frac{d^3}{{d x}^3}\, \left[ x \right] = \frac{d^2}{{d x}^2} \left[1\right] = \frac{d}{{d x}} \left[0 \right] = 0`.

Similarly,
`\displaystyle \frac{d^3}{{d x}^3} \left[70\right] = 0`.

Substitute these back to the expression of
`f^(\prime\prime\prime)(x)`.

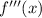`\begin{aligned} f^(\prime\prime\prime) &= 22\, \underbrace{\left(\frac{d^3}{{d x}^3}\left[x^3\right]\right)}_(6) + \underbrace{28\, \left(\frac{d^3}{{d x}^3} \left[x^2\right]\right)}_0 + \underbrace{55\, \left(\frac{d^3}{{d x}^3} \left[x\right]\right)}_0 + \underbrace{\frac{d^3}{{d x}^3} \left[70\right]}_0 \\ &= 22 * 6 \\ &= 132\end{aligned}`.