Question

Please answer the question that is in the photo attached below

Answer 1

7

Explanation:

Use Pythagorean Theorem:

A² + B² = C²

3² + B² = 4²

9 + B² = 16

B² = 7

B = √7

Answer 2

`\huge\boxed{b=√(7)}`

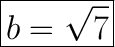
Explanation:

In order to solve for this equation we have to note a couple of things.

There is a diagonal square inside a larger square. The space formed by the smaller square not being in the larger square is a right triangle.

The side length of the smaller square (4) is also the hypotenuse of this triangle.

Since we know that the other side length of the triangle is 3, we can use the Pythagorean Theorem to find the value of b.

The Pythagorean Theorem states that
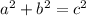`a^2 + b^2 = c^2`, where a and b are the legs and c is the hypotenuse.

We can substitute 3 in as a and 4 in as c and find b.

`3^2 + b^2 = 4^2`

`9+b^2=16`

`b^2=7`

`b = √(7)`

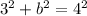
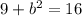
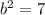
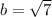
So b is
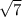`√(7)` units long.

Hope this helped!