Question

It is possible to test if a quadrilateral is a square by performing calculations on its diagonals, in this case, AC and BD. a quadrilateral is a square if all three of the following conditions are true

The diagonals intersect at their midpoints.

The diagonals are both the same length.

The diagonals are perpendicular.

Based on this information, is the figure below a square?


If so, give the results of all calculations that allow you to verify that it is.

If it is not a square, describe which condition or conditions are not met.

Answer 1

The figure is not a square, because:

The diagonals DO NOT intersect at their midpoints.

The diagonals are NOT of the same length.

The diagonals are NOT perpendicular.

Explanation:

✍️If two diagonals intersect at their midpoints, the coordinates of their midpoints will be the same.

Find the midpoints of diagonal AC and BD using the midpoint formula,
`M((x_1 + x_2)/(2), (y_1 + y_2)/(2))`.

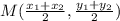Midpoint (M) of AC, for A(-4, -6) and C(6, -18):

`M((-4 + 6)/(2), (-6 + (-18))/(2))`

`M((2)/(2), (24)/(2))`

`M(1, 12)`

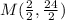
Midpoint of diagonal AC = (1, 12)

Midpoint (M) of BD, for B(-12, -12) and D(13, -1):

`M((-12 + 13)/(2), (-12 +(-1))/(2))`

`M((1)/(2), (-13)/(2))`

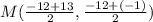
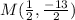
Midpoint of diagonal BD =
`M((1)/(2), (-13)/(2))`

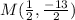
The coordinates of the midpoint of diagonal AC and diagonal BD are not the same, therefore, the diagonals do not intersect at their midpoints.

✍️Use distance formula to calculate the length of each diagonal to determine whether they are of the same length.

Distance between A(-4, -6) and C(6, -18):

`AC = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

`AC = √((6 -(-4))^2 + (-18 -(-6))^2)`

`AC = √((10)^2 + (-12)^2)`

`AC = √(100 + 144) = √(244)`

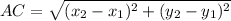
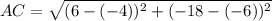
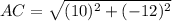
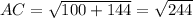
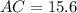`AC = 15.6` (nearest tenth)

Distance between B(-12, -12) and D(13, -1):

`BD = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

`BD = √((13 - (-12))^2 + (-1 -(-12))^2)`

`BD = √((25)^2 + (11)^2)`

`BD = √(625 + 121) = √(746)`

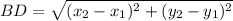
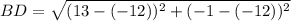
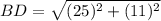
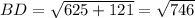
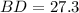`BD = 27.3` (nearest tenth)

Diagonal AC and BD are not of the same length.

✍️If the diagonals are perpendicular, the product of their slope would equal -1.

Slope of diagonal AC:

A(-4, -6) and C(6, -18)

`slope = (y_2 - y_1)/(x_2 - x_1) = (-18 -(-6))/(6 -(-4)) = (-12)/(10) = -(6)/(5)`

Slope of diagonal BD:

B(-12, -12) and D(13, -1)

`slope = (y_2 - y_1)/(x_2 - x_1) = (-1 -(-12))/(13 - (-12)) = (11)/(25)`

Product of their slope:

`-(6)/(5)*(11)/(25) = (66)/(125)`

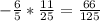
The product of their slope doesn't equal -1. Therefore, diagonal AC and BD are not perpendicular to each other.