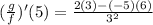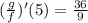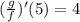Answer: a) -24
b)
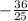
c) 4
Explanation:
a) To determine the value of (fg)', use the product rule of derivative, i.e.:
(fg)'(x) = f'(x)g(x) + f(x)g'(x)
(fg)'(5) = f'(5)g(5) + f(5)g'(5)
(fg)'(5) = 6(-5) + 3(2)
(fg)'(5) = -24
b) The value is given by the use of the quotient rule of derivative:
![((f)/(g))'(x)=(f'(x)g(x)-f(x)g'(x))/([g(x)]^2)](https://img.qammunity.org/2021/formulas/mathematics/college/udzkys1hn1qf4bb8wdh4m6qo8p2clngx3v.png)
![((f)/(g))' (5)=(f'(5)g(5)-f(5)g'(5))/([g(5)]^2)](https://img.qammunity.org/2021/formulas/mathematics/college/3ds0o0t69exx22xwacmg14s1dushi1038r.png)
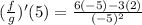
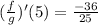
c)
![((g)/(f))'(5)=(g'(5)f(5)-g(5)f'(5))/([f(5)]^(2))](https://img.qammunity.org/2021/formulas/mathematics/college/n1vj4dq137i9gvd6ozqkg4qrkwecla1xbe.png)