The complete question is
Use implicit differentiation to find an equation of the tangent line to the curve at the given point.
 ,
,
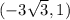
Answer:
Equation of tangent is y =
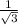 x + 4
x + 4
Explanation:
We are given the equation
 ,
,
upon differentiating
d(
 ) /dx = d(4)/dx
) /dx = d(4)/dx
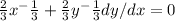
dy/dx =
 =
=
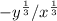
upon substituting the values (x, y)=
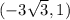
dy/dx =
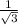
equation of the tangent
y - 1 =
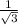 ( x- (-
( x- (-
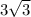 ))
))
y =
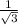 x + 4
x + 4