Answer:
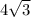
Explanation:
Since <PDA is right, the vertical angle, <BDC is right as well. Using sum of angles in a triangle, the angles in triangle BDC sum to 180, and for solving for <DCB, you get 30 degrees.
The line connecting the intersection of the tangents to the radius bisects the angle formed by the tangents; therefore, m<PCA is also 30 degrees.
A radius drawn to the point of tangency is perpendicular to the tangent, so <PAC is a right triangle. We can use sum of angles in a triangle for triangle PAC. Since <PCA is 30 and <PAC is right, <DPA is 60 degrees.
Now, we can look at triangle DPA, using sum of angles in a triangle, we can conclude triangle DPA is a 30-60-90 special right triangle. The leg opposite the 60 degree angle is √3 times the leg opposite the thirty degree angle. Since <DPA is 60 degrees and <PAD is 30:
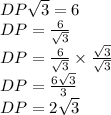
Also, in a 30-60-90, the hypotenuse is twice the leg opposite the 30 degree angle, so x is 2 * 2√3. or
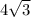 .
.